Reconstruction of Large, Irregularly Sampled Multidimensional Images. A Tensor-Based Approach.
Abstract
Many practical applications require the reconstruction of images from irregularly sampled data. The spline formalism offers an attractive framework for solving this problem; the currently available methods, however, are hard to deploy for large-scale interpolation problems in dimensions greater than two (3-D, 3-D+time) because of an exponential increase of their computational cost (curse of dimensionality). Here, we revisit the standard regularized least-squares formulation of the interpolation problem, and propose to perform the reconstruction in a uniform tensor-product B-spline basis as an alternative to the classical solution involving radial basis functions. Our analysis reveals that the underlying multilinear system of equations admits a tensor decomposition with an extreme sparsity of its one dimensional components. We exploit this property for implementing a parallel, memory-efficient system solver. We show that the computational complexity of the proposed algorithm is essentially linear in the number of measurements and that its dependency on the number of dimensions is significantly less than that of the original sparse matrix-based implementation. The net benefit is a substantial reduction in memory requirement and operation count when compared to standard matrix-based algorithms, so that even 4-D problems with millions of samples become computationally feasible on desktop PCs in reasonable time. After validating the proposed algorithm in 3-D and 4-D, we apply it to a concrete imaging problem: the reconstruction of medical ultrasound images (3-D+time) from a large set of irregularly sampled measurements, acquired by a fast rotating ultrasound transducer.
The manuscript is accepted for publication in IEEE Transactions on Medlical Imaging (access to preprint).
A set of images visualizing the results of the evaluation of the proposed reconstruction algorithm on standard regularly sampled 3-D datasets. All datasets were reconstructed from 20% of samples with highest values of the Laplacian.

 (a)
(b)
(a)
(b)
Figure 1. The Engine dataset. (a) original data, (b) reconstructed data
 (a)
(b)
(a)
(b)
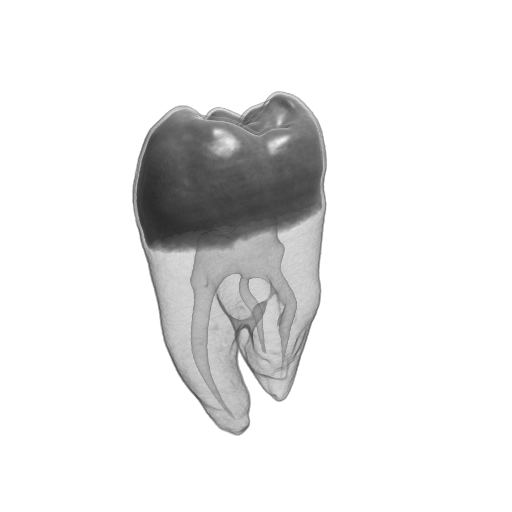
Figure 2. The Tooth dataset. (a) original data, (b) reconstructed data

 (a)
(b)
(a)
(b)
Figure 2. The Carp dataset. (a) original data, (b) reconstructed data

Figure 3. Visualization of the reconstruction of the Blunt-Fin dataset defined on a highly anisotropic curvilinear grid. The reconstruction grid has size 186x72x50, regularization tradeoff is 0.1, RMSE1 = 0.945%
This movie visualizes the result of the evaluation of the proposed algorithm applied to the reconstruction of a 4-D MRI dataset from 30% of randomly selected samples. The movie compares the result of the reconstruction (right) with the original dataset (left).
This movie provides a space-time visualization of the result of the reconstruction of a real-world 4-D arbitrarily sampled medical ultrasound data acquired by a fast continuously rotating ultrasound transducer. This particular dataset represents the motion of the left ventricle of the heart.